Garrett Lisi and E8: “The universe is maximally beautiful.”
Don Knuth: importunate permutation

The wonderful Cliff Stoll presents a Steiger Millionaire challenge; always offering me Acme Klein Bottles and his peculiar brand of crystal ball.


Consider the factored integers N=[(0), (1), (2), (3), (2,2), 5, (2,3), 7, (2,2,2)...], with each factor representing a point in Euclidean space. Each of these points is at a distance d from the origin, and can be ordered by d.
-- Ieso.hs
-- Integers in Euclidean space order
-- Uses the Haskell Number Theory functions, from the "Haskell for Maths"
-- site: http://www.polyomino.f2s.com/david/haskell/numbertheory.html
import Data.List
import Primes
-- Return distance between two points in Euclidean space. Points are lists
-- of possibly unequal lengths, padded with zeros as needed.
dist_points x y = sqrt (realToFrac ((foldl (+) 0 (map sq (zipWith (-) x1 y1)))))
where x1 = pad (lengthLongest [x,y]) x
y1 = pad (lengthLongest [x,y]) y
sq x = x * x
lengthLongest l = maximum (map length l)
pad len x = (x ++ zeroPadding)
where zeroPadding = genericTake (len - genericLength x) (repeat 0)
-- Return list of all prime factors of n
primeFactors 1 = [1]
primeFactors n = flatten (map expandedFactors (primePowerFactors n))
where
expandedFactors x = genericTake (snd x) (repeat (fst x))
flatten :: [[a]] -> [a]
flatten = foldl (++) []
-- Return distance between two factored integers
distance n m = dist_points (primeFactors n) (primeFactors m)
-- Return list of distances between origin and integers up to n,
-- sorted by distance d. Where ties occur, the lowest n comes first, i.e.,
-- where d=5 for both n=48 and n=5, the order is ... 5, 48 ....
-- Neil Sloane has suggested a different way of breaking ties is use of
-- lexicographic order, ie for n=48 [2,2,2,3] comes before n=5 [5] - see
-- below.
distanceOrigin n = map snd (sort d)
where
d = [(distance 0 i, i) | i <- [0..n]]
-- In order to list the integers within a certain distance d from the origin,
-- we have to calculate distances up to 2^(d^2/4), e.g. to list ALL
-- integers within a distance of 10, use range 2...2^25.
-- I believe a list is "complete" up to where a power of 2 appears,
-- because numbers greater than that power of 2 can't be closer
-- to the origin (except ties, depending on they are handled). However,
-- I am curious about how to determine the minimum number of
-- integers you have to calculate in order to make a list complete,
-- e.g., how high do we have to look to be sure we've found the
-- 20 integers closest to the origin?
main = do
-- Calculate integers within ~7 units of origin
print "n ordering for ties"
let d = [(distance 0 i, i) | i <- [0..8192]]
print (map snd (sort d))
-- Recalculate using lexicographic order to break ties
print "lexicographical ordering for ties"
let l = [(distance 0 i, primeFactors i, i) | i <- [0..8192]]
print (map lastx (sort l))
where
lastx (x, y, z) = z
For example, d=8.66 for N=125 at the point (5,5,5), while d=5.29 for N=128 at (2,2,2,2,2,2,2) :
*Ieso> distance 0 125 8.660254037844387 *Ieso> distance 0 128 5.291502622129181
Here is a simple view of several of these integers that lie in 3-space, with the distance between the origin and N=125 highlighted.
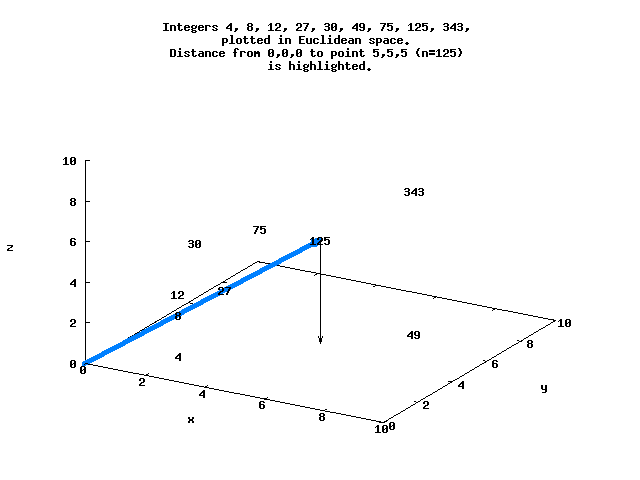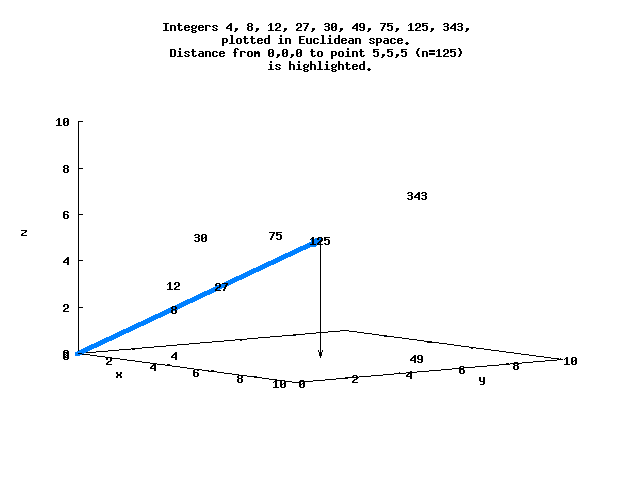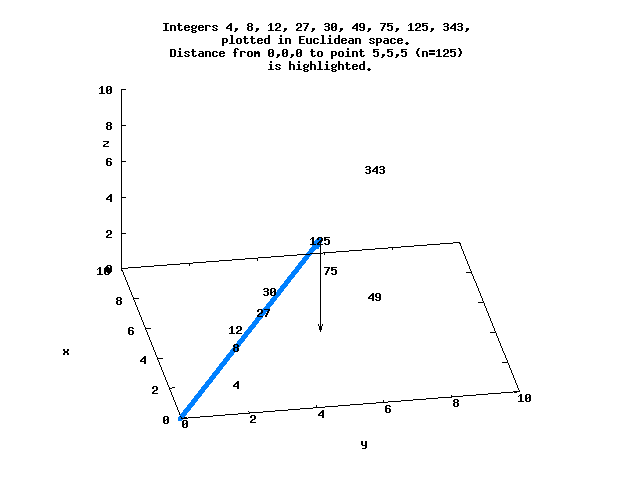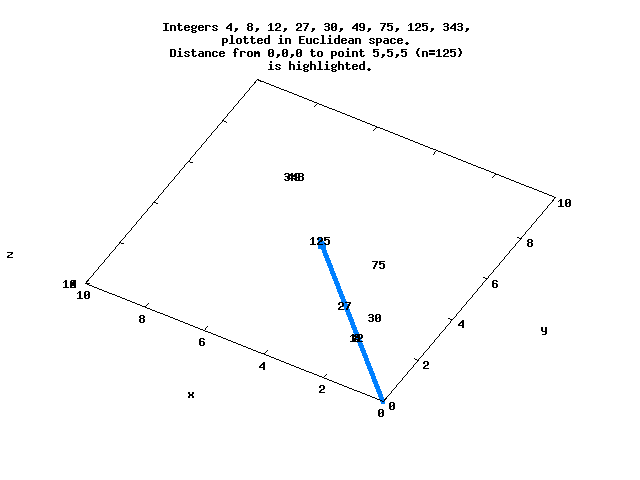
The sequence N=[0..8192] in Euclidean space ordered by d begins
*Ieso> distanceOrigin 8192 0,1,2,4,3,8,6,16,12,9,32,24,18,64,5,48,36,27,128,10,96,72,54,256,20,192,15,144,108,81,512,40,384,30,288,216,162,1024
(One way to think about this may be that integers with higher Ω(n) should be relatively clustered around the origin).
(The sequence is listed as OEIS A168521).
Who hath desired the Sea? — the sight of salt water unbounded –
The heave and the halt and the hurl and the crash of the comber wind-hounded?
The sleek-barrelled swell before storm, grey, foamless, enormous, and growing –
Who hath desired the Sea? — the immense and contemptuous surges?
The shudder, the stumble, the swerve, as the star-stabbing bow-sprit emerges?
Who hath desired the Sea? Her menaces swift as her mercies?
The in-rolling walls of the fog and the silver-winged breeze that disperses?
Who hath desired the Sea? Her excellent loneliness
Rather than forecourts of kings?
- Kipling
“It can get bitter on these heights, and the winds, how they blow. There has been many a roaring night Hector and I have thought we would perish on this Hill, but, of course, how could we? What comfort is the hearth fire without raw weather howling outside the door, and what pleasure is there in rest unless the day’s toil was almost more than you could bear?”
“Which were your greatest storms?” I asked.
He furrowed his brow. “We’ve had so many,” he spoke slowly, “and each comes upon us afresh, as if it never had a predecessor. It is a curious truth that I cannot remember the snows here in any particular…at night, it is not these storms that I dream about, but always springtimes and storms below. In my dreams, I forget my century in heaven and recall only my few springtimes on earth.”
– Donald McCaig
Old journal entries, May 21, 2003, West Desert, Utah
Cottonwood, graves, and light.
The raw native sandstone, faintly inscribed.
Granite black, etched roses. Ruby Young Fowler, May 6, 1891 – April 1, 1918, “Beloved Mother”.
Dove in sandstone. “In memory of Mary E. Young”, born Dec 30, 1871, died Dec 17th 1880, “…farewell my dear…no longer must I stay.”
“In memory of Leroy Young, son of B and Mary E. Young, born Oct 15th 1867, died Nov 30th 1880. “Weep not for me.”
“Ray G, son of E & M Heckethorn, Dec 17, 1884 – May 15, 1911″ – “The angels called him.”
“Eugene L. Son of RC & L Heckethorn, April 15, 1909, June 6, 1911. Darling we miss thee.”
Then next day the journey through heat and light to Crystal Peak.
After years of seeing the mountain from afar, from over horizons, I am here.
Silence. Stillness, except my mind.
Warm yellow glow on startling white; improbable peak.
Oh how I wish I were free.


Click here to donate to relief efforts in areas hit hard by Typhoon Morakot.
There, where love awakens, dies the I, dark despot.
Dr. John Archibald Wheeler, contemporary of Bohr, teacher of Feynman and generations of other physicists, died on Sunday.
There is a wonderful tribute to him at Cosmic Variance.
Here is the dedication to his landmark textbook, Gravitation (with Charles Misner and Kip Thorne):
We dedicate this book
To our fellow citizens
Who, for love of truth,
Take from their own wants
By taxes and gifts,
And now and then send forth
One of themselves
As dedicated servant,
To forward the search
Into the mysteries and marvelous simplicities
Of this strange and beautiful Universe,
Our home.
Three days ago Hu Jia (胡佳) was sentenced to 3+ years in prison for his ongoing, courageous criticisms of the government of the People’s Republic of China.
His wife, fellow activist Zeng Jinyan (曾金燕), maintains a blog here.
Please contact me if you’d like to help send assistance to Jia and his family.
At the recent 2008 TED conference in Monterey, Clifford Stoll ended his wonderful talk with these words inscribed on the Hayes Clock Tower bell at SUNY:
All truth is one.
In this light
may science and religion endeavor here
for the steady evolution of mankind.
From darkness to light,
from narrowness to broadmindedness,
from prejudice to tolerance.
It is the voice of life which calls us to come and learn.