Garrett Lisi and E8: “The universe is maximally beautiful.”
Don Knuth: importunate permutation

The wonderful Cliff Stoll presents a Steiger Millionaire challenge; always offering me Acme Klein Bottles and his peculiar brand of crystal ball.


Consider the factored integers N=[(0), (1), (2), (3), (2,2), 5, (2,3), 7, (2,2,2)...], with each factor representing a point in Euclidean space. Each of these points is at a distance d from the origin, and can be ordered by d.
-- Ieso.hs
-- Integers in Euclidean space order
-- Uses the Haskell Number Theory functions, from the "Haskell for Maths"
-- site: http://www.polyomino.f2s.com/david/haskell/numbertheory.html
import Data.List
import Primes
-- Return distance between two points in Euclidean space. Points are lists
-- of possibly unequal lengths, padded with zeros as needed.
dist_points x y = sqrt (realToFrac ((foldl (+) 0 (map sq (zipWith (-) x1 y1)))))
where x1 = pad (lengthLongest [x,y]) x
y1 = pad (lengthLongest [x,y]) y
sq x = x * x
lengthLongest l = maximum (map length l)
pad len x = (x ++ zeroPadding)
where zeroPadding = genericTake (len - genericLength x) (repeat 0)
-- Return list of all prime factors of n
primeFactors 1 = [1]
primeFactors n = flatten (map expandedFactors (primePowerFactors n))
where
expandedFactors x = genericTake (snd x) (repeat (fst x))
flatten :: [[a]] -> [a]
flatten = foldl (++) []
-- Return distance between two factored integers
distance n m = dist_points (primeFactors n) (primeFactors m)
-- Return list of distances between origin and integers up to n,
-- sorted by distance d. Where ties occur, the lowest n comes first, i.e.,
-- where d=5 for both n=48 and n=5, the order is ... 5, 48 ....
-- Neil Sloane has suggested a different way of breaking ties is use of
-- lexicographic order, ie for n=48 [2,2,2,3] comes before n=5 [5] - see
-- below.
distanceOrigin n = map snd (sort d)
where
d = [(distance 0 i, i) | i <- [0..n]]
-- In order to list the integers within a certain distance d from the origin,
-- we have to calculate distances up to 2^(d^2/4), e.g. to list ALL
-- integers within a distance of 10, use range 2...2^25.
-- I believe a list is "complete" up to where a power of 2 appears,
-- because numbers greater than that power of 2 can't be closer
-- to the origin (except ties, depending on they are handled). However,
-- I am curious about how to determine the minimum number of
-- integers you have to calculate in order to make a list complete,
-- e.g., how high do we have to look to be sure we've found the
-- 20 integers closest to the origin?
main = do
-- Calculate integers within ~7 units of origin
print "n ordering for ties"
let d = [(distance 0 i, i) | i <- [0..8192]]
print (map snd (sort d))
-- Recalculate using lexicographic order to break ties
print "lexicographical ordering for ties"
let l = [(distance 0 i, primeFactors i, i) | i <- [0..8192]]
print (map lastx (sort l))
where
lastx (x, y, z) = z
For example, d=8.66 for N=125 at the point (5,5,5), while d=5.29 for N=128 at (2,2,2,2,2,2,2) :
*Ieso> distance 0 125 8.660254037844387 *Ieso> distance 0 128 5.291502622129181
Here is a simple view of several of these integers that lie in 3-space, with the distance between the origin and N=125 highlighted.
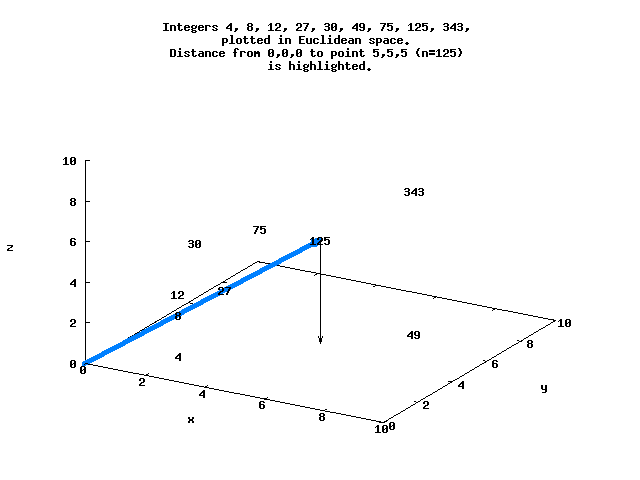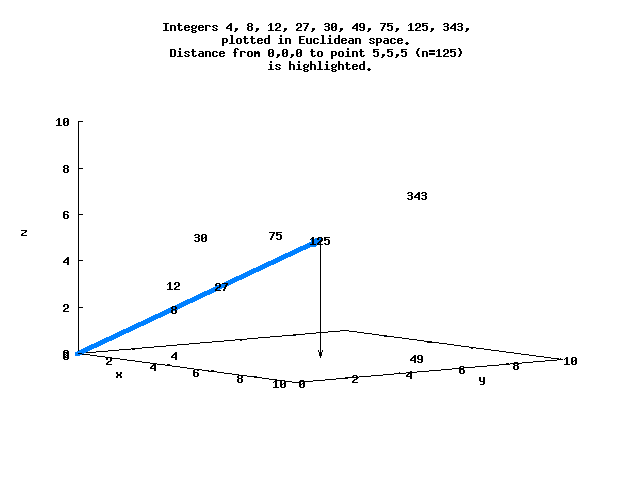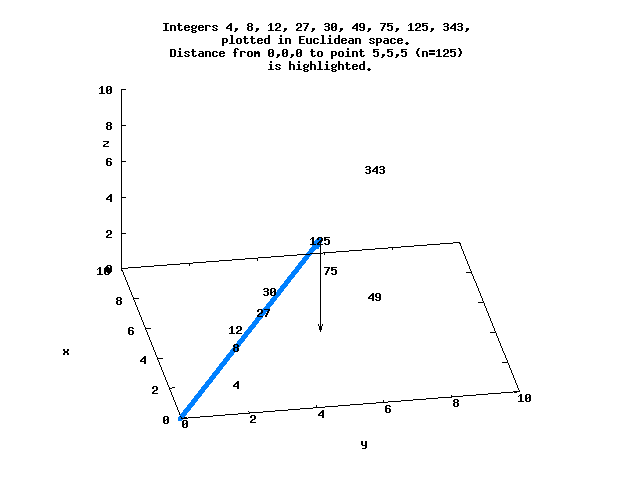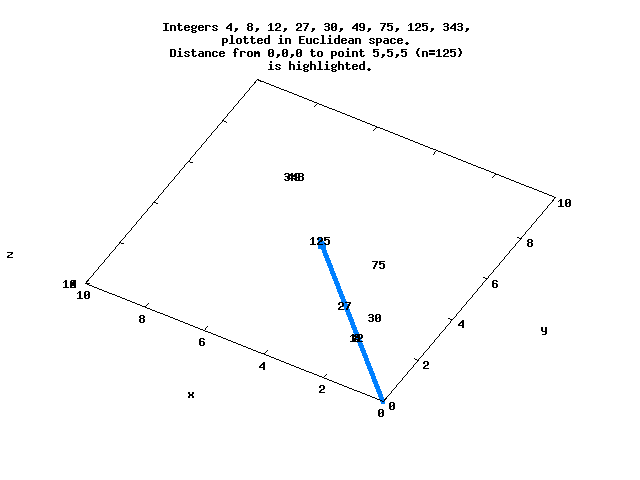
The sequence N=[0..8192] in Euclidean space ordered by d begins
*Ieso> distanceOrigin 8192 0,1,2,4,3,8,6,16,12,9,32,24,18,64,5,48,36,27,128,10,96,72,54,256,20,192,15,144,108,81,512,40,384,30,288,216,162,1024
(One way to think about this may be that integers with higher Ω(n) should be relatively clustered around the origin).
(The sequence is listed as OEIS A168521).