Consider the factored integers N=[(0), (1), (2), (3), (2,2), 5, (2,3), 7, (2,2,2)...], with each factor representing a point in Euclidean space. Each of these points is at a distance d from the origin, and can be ordered by d.

-- Ieso.hs
-- Integers in Euclidean space order

-- Uses the Haskell Number Theory functions, from the "Haskell for Maths"
-- site: http://www.polyomino.f2s.com/david/haskell/numbertheory.html
import Data.List
import Primes

-- Return distance between two points in Euclidean space. Points are lists 
-- of possibly unequal lengths, padded with zeros as needed.
dist_points x y = sqrt (realToFrac ((foldl (+) 0 (map sq (zipWith (-) x1 y1)))))
           where x1 = pad (lengthLongest [x,y]) x
                 y1 = pad (lengthLongest [x,y]) y
                 sq x = x * x
                 lengthLongest l = maximum (map length l)
                 pad len x = (x ++ zeroPadding) 
                     where zeroPadding = genericTake (len - genericLength x) (repeat 0)

-- Return list of all prime factors of n
primeFactors 1 = [1]
primeFactors n = flatten (map expandedFactors (primePowerFactors n))
            where
              expandedFactors x = genericTake (snd x) (repeat (fst x))
              flatten :: [[a]] -> [a]
              flatten = foldl (++) []

-- Return distance between two factored integers 
distance n m = dist_points (primeFactors n) (primeFactors m)

-- Return list of distances between origin and integers up to n,
-- sorted by distance d. Where ties occur, the lowest n comes first, i.e., 
-- where d=5 for both n=48 and n=5, the order is ... 5, 48 ....
-- Neil Sloane has suggested a different way of breaking ties is use of 
-- lexicographic order, ie for n=48 [2,2,2,3] comes before n=5 [5] - see
-- below.
distanceOrigin n = map snd (sort d)
                   where
                     d = [(distance 0 i, i) | i <- [0..n]]

-- In order to list the integers within a certain distance d from the origin,
-- we have to calculate distances up to 2^(d^2/4), e.g. to list ALL 
-- integers within a distance of 10, use range 2...2^25.

-- I believe a list is "complete" up to where a power of 2 appears, 
-- because numbers greater than that power of 2 can't be closer 
-- to the origin (except ties, depending on they are handled). However, 
-- I am curious about how to determine the  minimum number of 
-- integers you have to calculate in order to make a list complete, 
-- e.g., how high do we have to look to be sure we've found the
-- 20 integers closest to the origin? 

main = do
  -- Calculate integers within ~7 units of origin
  print "n ordering for ties"
  let d = [(distance 0 i, i) | i <- [0..8192]]
  print (map snd (sort d))

  -- Recalculate using lexicographic order to break ties
  print "lexicographical ordering for ties"  
  let l = [(distance 0 i, primeFactors i, i) | i <- [0..8192]]
  print (map lastx (sort l))
        where
          lastx (x, y, z) = z
 

For example, d=8.66 for N=125 at the point (5,5,5), while d=5.29 for N=128 at (2,2,2,2,2,2,2) :

*Ieso> distance 0 125
8.660254037844387
*Ieso> distance 0 128
5.291502622129181

Here is a simple view of several of these integers that lie in 3-space, with the distance between the origin and N=125 highlighted.

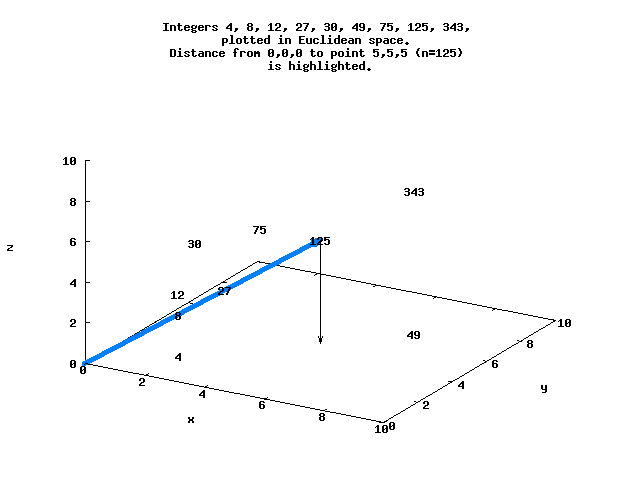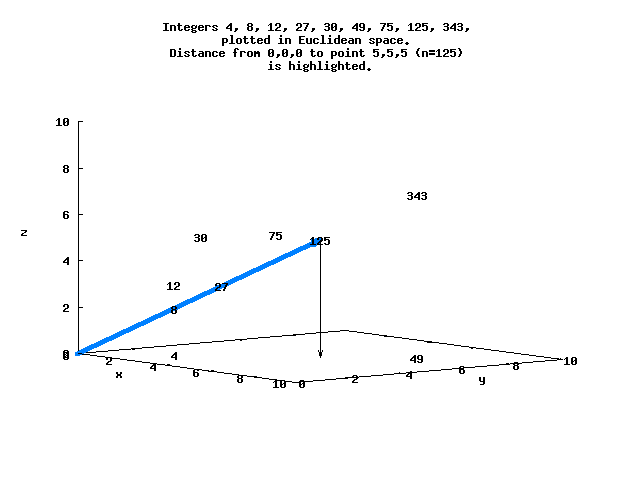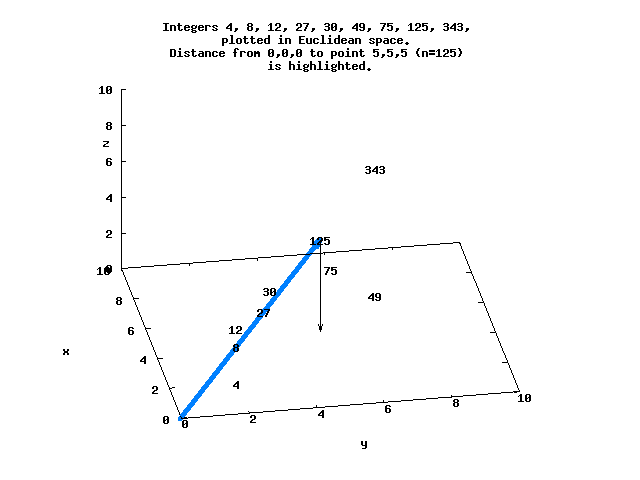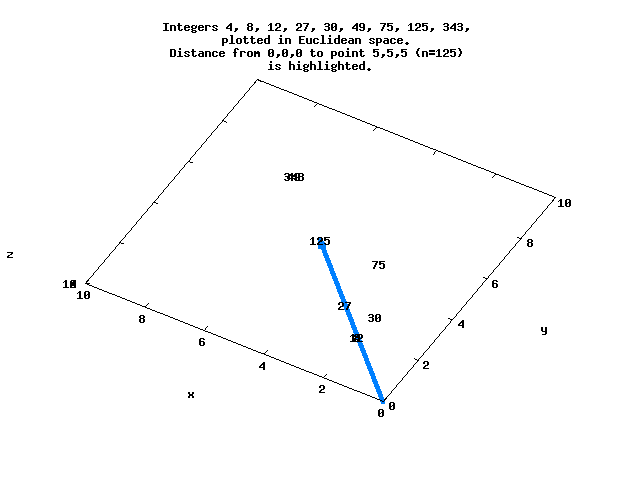
The sequence N=[0..8192] in Euclidean space ordered by d begins

 
*Ieso> distanceOrigin 8192
0,1,2,4,3,8,6,16,12,9,32,24,18,64,5,48,36,27,128,10,96,72,54,256,20,192,15,144,108,81,512,40,384,30,288,216,162,1024

(One way to think about this may be that integers with higher Ω(n) should be relatively clustered around the origin).

(The sequence is listed as OEIS A168521).